Project-Based Instruction (PBI) is a teaching approach that engages students in meaningful, authentic learning through a central driving question that encourages exploration, collaboration, and problem-solving. Rather than relying on traditional lectures, PBI emphasizes hands-on inquiry, student choice, and the creation of products that demonstrate deep understanding. Throughout the semester, the course offered a full, immersive look at what it takes to design and implement this type of instruction. Trial and error during field experiences revealed which strategies supported student engagement, such as assigning clear roles, encouraging productive discussion, and connecting tasks to students' interests, as well as which areas required adjustment, including pacing and anticipating potential misconceptions. The structure of the course, combined with consistent feedback from instructors, mentor teachers, teaching partners, AI tools, and reflective practice, highlighted the strengths and areas for growth involved in facilitating PBI. Overall, the experience demonstrated how PBI can strengthen student motivation, build confidence, and create a more student-centered classroom environment, while also helping developing educators refine their teaching practices in meaningful and practical ways.

My field experience took place during 5th and 6th periods, working with an Honors Geometry class and a Math for Liberal Arts class. Throughout the placement, I worked closely with my teaching partner, Darcy Rosa, and together we collaborated on most lesson plans and classroom activities. While many lessons were delivered jointly, there were also a few instances where I took the lead in the Geometry class, and Darcy led instruction in the other. The sections below outline the dates and key activities for each session, along with a sample lesson plan that provides a detailed, structured look at the geometry instruction implemented during our experience.
During the first field experience, the main goal was to observe the classroom, meet the teacher and students, learn daily procedures, and understand the classroom management style. As I observed, I focused on details like time management, technology use, and the overall learning environment. My mentor teacher, Mrs. Wishin, maintained a clear and structured approach to her lessons. She used a stopwatch displayed on the board to help pace the class and ensure all planned activities were completed. I also noticed that each student had a school-issued laptop for academic use, which ensured consistent, efficient access to technology.
The classroom environment felt positive, calm, and encouraging. Pastel colors helped create a welcoming atmosphere, and the decorations were purposeful rather than overwhelming. Student-made posters displayed geometric rules, key ideas, classroom expectations, and examples of classwork. While there weren’t many traditional math posters, most visual elements focused on student growth and motivation. On the board, the academic standards and current content were clearly listed, and additional posters from interactive activities highlighted students’ expectations for the course and their reflections on the class.
During the second field experience, I continued in an observer role but also had the opportunity to help create and lead an icebreaker activity. Our goal was to establish a stronger introduction and begin building connections with the students. We designed a fun activity where each student introduced themselves and shared an animal or food that started with the same letter as their first name. The document below highlights all the creative and entertaining responses students came up with.
This session also gave us a deeper look into our mentor teacher’s instructional style. She organizes seating in groups of four, which supports collaboration and hands-on learning. She regularly encourages group-based activities that shift the focus away from traditional lectures and toward a more student-centered classroom environment. We also began noticing her attention signals and her grading approach, which incorporates peer grading, group participation points, and recognition of student improvement.
During our next classroom interaction, we began to warm up more with the students by introducing a fun bell ringer activity. Since the class was already seated in groups of four, we designed the bell ringer as a quick, collaborative matching game. Each group received a small bag filled with slips of paper containing transversal angle pair theorems, their definitions, and corresponding diagrams. Their task was to match each theorem with the correct definition and visual, with the first group to finish accurately winning the game. Because students were just being introduced to this topic, we kept the activity simple and structured to last about 5–7 minutes. One of us led the explanation while the other handed out materials and checked each group’s work once they signaled they were done.
This activity also served as our first real opportunity to interact closely with the students, giving us time to learn their names, practice attention-getting cues, and observe how they communicated within their groups. We started to notice which students were more talkative, which were shy, and which were easily distracted, allowing us to get a feel for each personality. This helped us not only introduce the content engagingly but also begin building stronger classroom connections and better understand how to support students in future lessons.
During this field experience, we reached the point where we fully took over the classroom and implemented a complete project-based instruction lesson. For our first full class, we designed a detective-style crime scene activity aligned with the students’ geometry content. The goal was to help students review and apply key concepts from Chapters 3.1–3.3. Through collaborative “crime file” cases, students worked with corresponding, alternate interior, alternate exterior, same-side interior, and vertical angles while practicing how to justify their reasoning.
In this activity, students worked in groups to solve geometry “crime files,” each presenting different angle relationships and clues. Groups analyzed the evidence, used angle theorems to solve for missing measures, and justified each step of their process. Once all groups cracked their cases, they revealed a pair of clue letters that helped the class uncover a final secret message: “PATRICK IS GUILTY!” (inspired by our SpongeBob theme).
After the group work, we called on each team to present its solution. Students explained their answers, the theorems or postulates they applied, and how they solved for the unknown angles. As each group presented, we guided the class through evaluating the accuracy of the solution and checking whether their clue letters aligned with the secret code. Throughout the presentations, we facilitated discussion, addressed misconceptions, and highlighted correct examples of geometric reasoning.
For this field experience, we noticed how positively students responded to interactive learning, so we continued using game-based formative assessments to keep participation high. We also saw students becoming more comfortable with us each week, which made our activities even more engaging. For this session, we created a Jeopardy-style review game aligned with the upcoming assessment. I projected the game with three content categories and explained the rules before forming student teams. As we moved through each round, students answered collaboratively, and after all groups attempted a question, everyone raised their boards to reveal their responses. The main group selected for the round then explained their reasoning and showed their work. As each team presented, we guided the class in evaluating the accuracy of their solutions, addressing misconceptions, and reinforcing the correct use of geometric reasoning.
In the following field experience, we incorporated a classic game of charades into a lesson on geometric transformations. The goal of “Transformation Charades” was for students to demonstrate and identify translations and reflections using coordinate grids. This activity helped students apply transformation rules, visualize rigid motions, and articulate their reasoning while working collaboratively in a fun, competitive setting.
Instead of acting out clues, groups used drawings to represent transformations, encouraging them to apply rules and visualize rigid motions. After reviewing the steps and modeling an example, we organized students into groups and began the rounds. The winning team from each round came to the board to redraw their figure, explain the transformation they performed, and justify how they knew it matched the rule. This allowed us to address misconceptions, reinforce key vocabulary, and check for understanding in a fun, collaborative way.
This week was our fourth and final field experience leading the class, and our focus was on using technology to help students review for their exam. We incorporated two interactive activities to keep engagement high. For the bell ringer, we displayed a transformation memory game on the whiteboard with scrambled image cards and matching transformation rule cards. Students took turns selecting one image and one rule in an attempt to make a correct match. Whenever a match was made, we briefly discussed why it was accurate and how the transformation worked. The game continued until all pairs were matched.
For the main activity, we projected a Kahoot review covering all types of transformations learned in class. Students joined on their devices and competed individually. Between questions, we paused to address misconceptions and highlight key ideas to ensure the review remained both fun and meaningful. After each question, we checked the class results. If many students chose the wrong answer, we took a moment to re-explain the concept or provide another example on the board.
For my final day with this amazing class, we supported the teacher by assisting with her pre-planned lesson. Throughout the period, we helped Ms. Wishin as students worked through a series of stations, each focusing on a different part of the lesson. She explained that this structure allows her to pinpoint specific areas where students may be struggling since the content is broken into smaller, targeted tasks. Darcy and I served primarily as additional support, helping answer questions and guiding students as they moved through each station. With two extra sets of hands in the room, more student questions could be addressed, and Ms. Wishin shared that having this support was extremely helpful to her. This final day also allowed us to reflect on how much we had learned about this class, ranging from the students’ personalities and learning styles to the flow and demands of a high school environment. We recognized our own strengths and weaknesses in real time. We received meaningful feedback from our mentor teacher, which gave us a clearer understanding of how to continue growing as future educators.

The following student artifact came from our Math for Liberal Arts 6th-period class. This work sample is from an activity where students began exploring different equation forms, identifying vertices and zeros, and observing how changes in an equation affect the shape and position of its graph. In this task, students were challenged to sketch three different graphs based on the provided equations, which are also shown in the artifact. Our goal was to help them visually understand how altering components of an equation transforms its graph.
The main feedback we provided focused on labeling and organization. In the artifact, the student plotted all three graphs correctly, but it’s difficult for a viewer to tell which graph matches each equation. Clear labeling and tracking these changes are essential skills as geometry and algebraic reasoning become more advanced. However, we also noticed a positive aspect that isn’t shown directly in the artifact. The student took the time to choose four x-values, substitute them into each equation, calculate the corresponding y-values, and build a small table before graphing. This methodical approach shows strong foundational thinking, even if the final product needs clearer organization.

This artifact comes from the same activity as the one above. Like the previous student, this learner also struggled with labeling, making it unclear which graph corresponds to each equation. However, what stood out in this artifact is that the student went a step further by exploring how changing the x-values in the equation affected the graph’s movement. They took time to analyze how the graph shifted and in which direction, showing a deeper curiosity about how transformations occur within the equation.
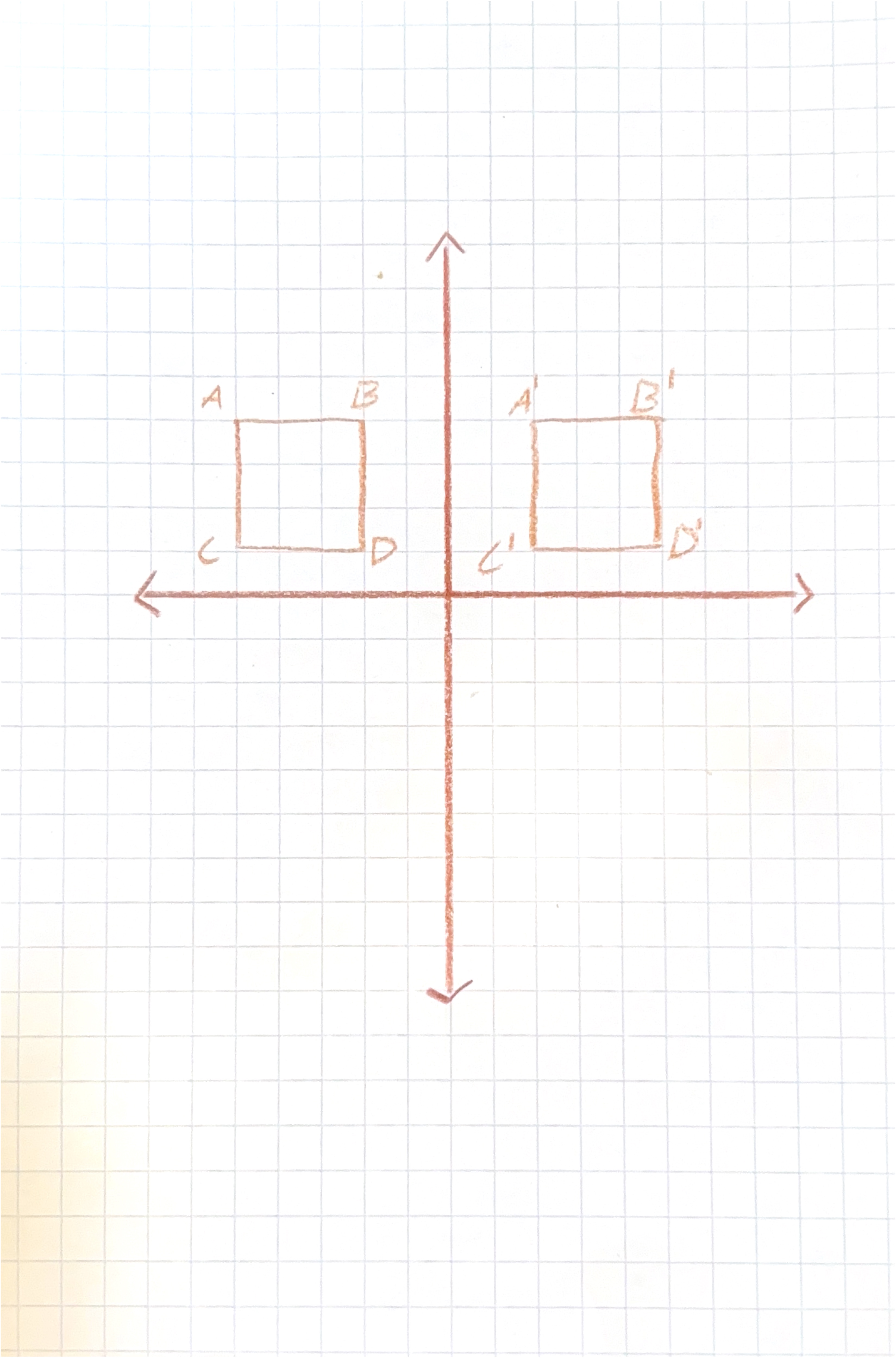


These artifacts come from our 5th-period geometry class on 10/30/25, when we conducted the geometry version of charades. Each sample shows what students drew for their groups to help them guess both the transformation and the specific transformation rule. One overall strength across all the artifacts is that students consistently labeled the pre-image and the transformed image, an essential step for helping their group identify the correct transformation.
However, only one group took the additional step of labeling each corresponding point. This becomes especially important as transformations become more advanced. For example, during rotations, the orientation of a shape changes, which can alter the position of each point. Labeling points clearly, such as A and A', from the start helps prevent confusion and avoids misconceptions as students move into more complex transformation work.
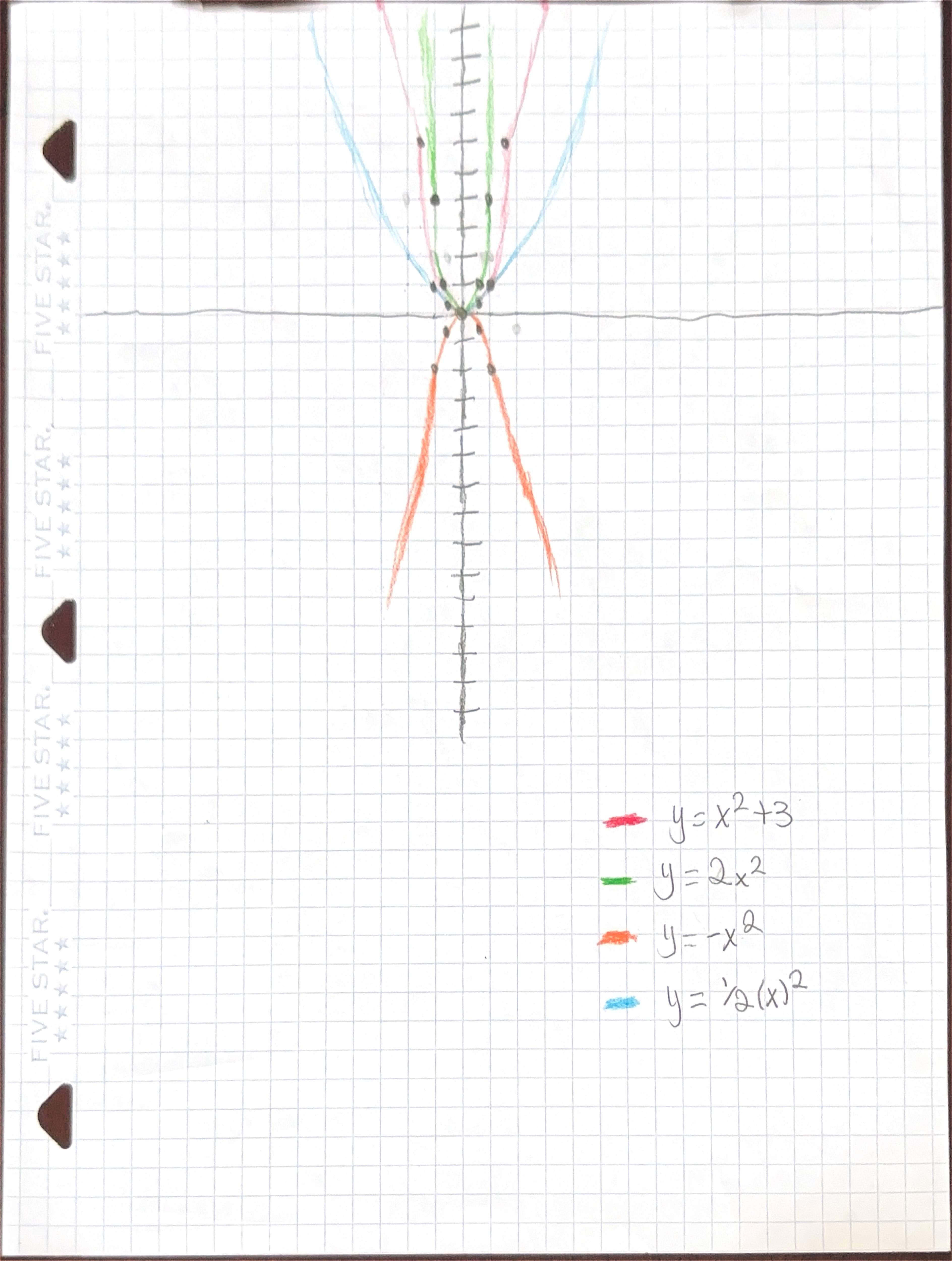
This final artifact comes from our last session with the 6th-period Math for Liberal Arts class. In this lesson, students continued exploring parabolas in standard form and how changes in the equation affect the graph. This work sample shows great improvement and understanding of the topic. The student correctly classified each equation to its corresponding graph, plotted coordinates accurately, and clearly demonstrated how the given equation transforms the parent function.
Purpose and Selection: These activities were chosen to review key concepts, such as geometric transformations and parabolas, in a fun, engaging way while providing immediate feedback on student understanding. Game-based assessments encouraged participation and allowed students to demonstrate mastery in a low-pressure environment.
Administration: For Jeopardy, I projected the game on the board and guided students in teams, collecting responses verbally and through whiteboards. For Kahoot, students joined individually on their devices, answering multiple-choice or visual questions in real-time.
Use of Data: Student responses were monitored after each question. When a majority of students answered incorrectly, we paused to clarify misconceptions or provide additional examples. This immediate feedback helped adjust the pace and focus of instruction to reinforce understanding.
Purpose and Selection: Activities like Transformation Charades and the detective crime scene were designed to help students apply geometric concepts such as transformations, angle relationships, and parallel lines with transversals. These formative assessments allowed students to demonstrate reasoning and problem-solving skills collaboratively.
Administration: Students worked in groups, using drawings or problem-solving at stations. In the charades activity, they drew transformations for peers to identify; in the crime scene, they analyzed “crime files” and justified their solutions. I circulated the classroom to observe, ask guiding questions, and collect group work as evidence.
Use of Data: Observing group interactions and reviewing artifacts allowed us to identify levels of understanding, misconceptions, and areas where additional guidance was needed. For example, we noted which groups properly labeled pre-images and transformed images, and which needed extra support to classify points correctly. This informed targeted feedback and instructional adjustments.